Kaip toli galite pamatyti meteorą?
>Gaunu el.
Dauguma užduoda įvairaus tipo klausimus, į kuriuos daugeliui gana paprasta atsakyti (iš tikrųjų į daug ką būtų galima atsakyti „Google“, užuominomis). Tačiau kartais sulaukiu klausimo, į kurį sunkiau atsakyti, ar net tokio, apie kurį galvojau apie save, bet niekada nesugebėjau išsiaiškinti.
Taigi aš buvau labai suintriguotas, kai gavau klausimą iš blogo skaitytojo Deano Lewiso apie meteorus. Per Perseidų meteorų lietų 2018 metais jis buvo toli nuo savo šeimos, atskirtas maždaug 1000 kilometrų. Jei jis pamatė meteorą, ar buvo įmanoma, kad jie matytų tą patį iš tolimesnės vietovės?
Paaugliai mutantai vėžliai nindziai 2 1991 m
Trumpas atsakymas yra: Taip! Ilgas atsakymas yra… matematika. Šauni, linksma matematika.
Ir matydamas, kaip, paskelbus šį straipsnį, 2018 m. Kasmet vykstančios „Geminid“ meteorų lietaus viršūnės šį vakarą, manau, kad tikslinga tai išsiaiškinti.
Avarijos kurso astronomija: Meteorai, Meteoroidai ir Meteoritai, Oh My!
Jei Žemė būtų visiškai plokščia, tada iš principo matytumėte meteorą iki bet kurio Žemės krašto. Kol esate virš žemės, net ir mažytis, jūsų matymo linija pasiekia kiekvieną kvadratinį centimetrą jūsų pusėje esančios planetos, todėl kiekvienas meteoras yra matomas visiems. Tiesą sakant, oras nėra visiškai skaidrus, todėl tam tikru atstumu žiūrite tiek daug purvo, kad nieko nematote.
Tačiau Žemė nėra plokščia. Rimtai! Tai apvalus. O atmosfera supa jį kaip kriauklę, plonėja su ūgiu ir galiausiai išnyksta; tas aukštis priklauso nuo jūsų erdvės apibrėžimo. Tačiau mes galime šiek tiek apgauti, nes žinome mokslą: tokie meteorai kaip dušai linkę sudegti maždaug 100 kilometrų virš žemės. Šis aukštis priklauso nuo daugelio dalykų, įskaitant tai, koks didelis meteoroidai (kietos tarpplanetinių šiukšlių dalys, sklindančios per erdvę) yra tai, kaip greitai jos juda, kokiu kampu patenka į atmosferą ir pan. Bet pavadinkime tai 100 km.
Artimiausias meteoras jums gali būti, jei esate tiesiai po juo, ir tada jis yra 100 km tiesiai (jūsų zenite). Jei jis sudegina toliau nuo zenito, tada jis turi būti toliau nuo jūsų. Toliausiai matote meteorą, todėl jis yra pagrįstas, jei jis yra tiksliai horizonte.
Jo geometrija atrodo taip (pastaba: NE pagal mastelį):
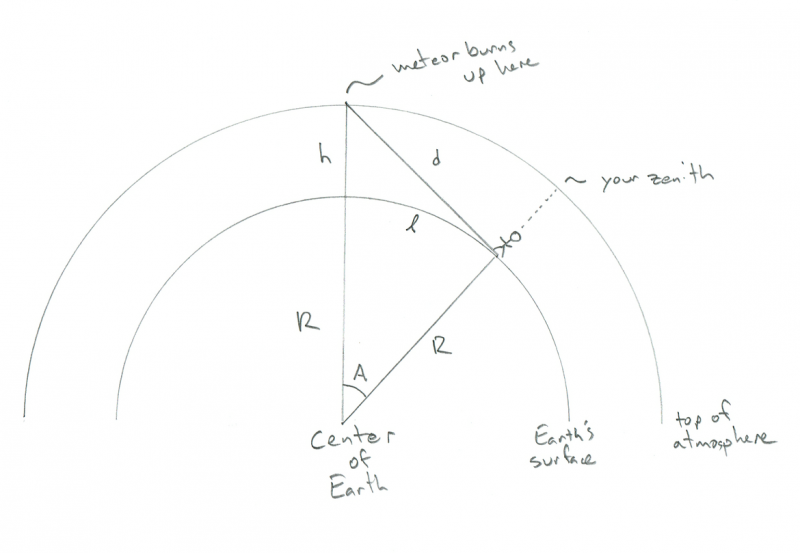
Schema, rodanti stebėtojo, stebinčio degantį meteorą, geometriją. Kreditas: Philas Plaitas
Jūs galite pamatyti mažą lazdos žmogų, stovintį išlenktos Žemės paviršiuje - tarkime, tai jūs - ir (taip pat išlenktą) atmosferą virš jų. Šioje diagramoje R yra Žemės spindulys (6400 km), h yra meteoro sudegimo aukštis (100 km), o d - atstumas nuo jūsų iki meteoro. A yra kampas tarp jūsų padėties Žemėje ir meteoro padėties virš jos, o kursyvas l (kaip ilgis) yra atstumas, kurį turite nueiti, kad meteoras būtų tiesiai virš galvos (aš žinau, kad tai atrodo keista norėti žinoti, bet pakęsti mane). Keista, bet jūs galite apskaičiuoti viską, ko jums reikia čia, nežinodami d, bet c'mon, šaunu žinoti, kaip toli yra meteoras, tiesa?
Svarbiausia yra pamatyti, kad kampas tarp meteoro, tavęs ir Žemės centro yra stačias. Taip yra todėl, kad meteoras yra horizonte, kaip jūs matote (arba, jei jums labiau patinka linksmas žargonas, liestinės linijoje vidiniame apskritime, kur R jį kerta). Tai daro trikampį stačiu trikampiu, o jei prisimenate vidurinės mokyklos matematiką, tai reiškia, kad galite rasti visas kraštines ir kampus!
Prisiminti Pitagoro teorema ? Stačiakampiame trikampyje hipotenuzės ilgio kvadratas yra lygus kitų dviejų kraštinių kvadratų sumai*. Mūsų trikampyje hipotenuzė yra R+h, o kitos kraštinės yra R ir d.
Taigi
(R+h)2= d2+ R.2
arba padauginus iš kairės pusės (naudokite FOLIJA ):
R2+ 2Rh + h2 = d2+ R.2
Išspręskite d, kad pamatytumėte, kaip toli nuo jūsų yra meteoras. Atminkite, kad R2 yra abiejose pusėse, todėl atšaukite juos, kad gautumėte
d2= 2Rh + h2
Arba
d = kvadratinė šaknis (2Rh + h2)
Na, mes žinome visus šiuos skaičius! „Plug-n-chug“, kūdikis:
d = kvadratinė šaknis (2 x 6400 x 100 + 10 000) = 1136 km
Aha! Tai reiškia, kad jei horizonte matote meteorą, jis yra už daugiau nei 1100 kilometrų! Tai ilgas kelias, ir techniškai toliausiai nuo žemės galite pamatyti meteorą.
Dabar suraskime kursyvųjį l. Pirmiausia turime žinoti kampą A. Tam reikalinga tam tikra trigonometrija. Yra daug trig tapatybes galite tai išsiaiškinti, bet mano mėgstamiausia†yra tai, kad stačiajame trikampyje kampo sinusas yra priešingos kraštinės ilgis, padalytas iš hipotenuzės ilgio. Taigi, jei gausime šį santykį, kampui gauti galime naudoti atvirkštinį sinusą (ar arciną).
sin (A) = d / (R + h)
buster scruggs tėvų vadovo baladė
taip
A = be-1(d / R + h)
„Plug-n-chug“ dar kartą, ir gaunu A = 10 °. Tai padorus Žemės paviršiaus fragmentas!
Ir dabar mes galime gauti kursyvų l. Aplink Žemę yra 360 °, o Žemės apskritimas yra 2 x pi x spindulys = 40 192 km, todėl yra
40 192 km / 360 ° = 112 kilometrų vienam laipsniui
o tai savo ruožtu reiškia 10 ° = 1120 kilometrų. Tai gana arti d, o tai nenuostabu. Piešiniai yra perdėti, tačiau iš tikrųjų oro apvalkalas virš mūsų yra mažas, palyginti su Žemės dydžiu. Jei padaryčiau brėžinius pagal mastelį, pamatytumėte, kad d ir l iš tikrųjų yra gana arti ilgio.
Gerai, tad kodėl aš karšta ir varginu, kad radau l? Dėl pirminio klausimo! Jei po visų matematikų pamiršote, tai kiek toli gali būti du žmonės ir vis tiek matyti tą patį meteorą?
Tokiu atveju meteoras būtų tiesiai tarp jų ir kiekviename jų horizonte. Geometrija atrodo taip:
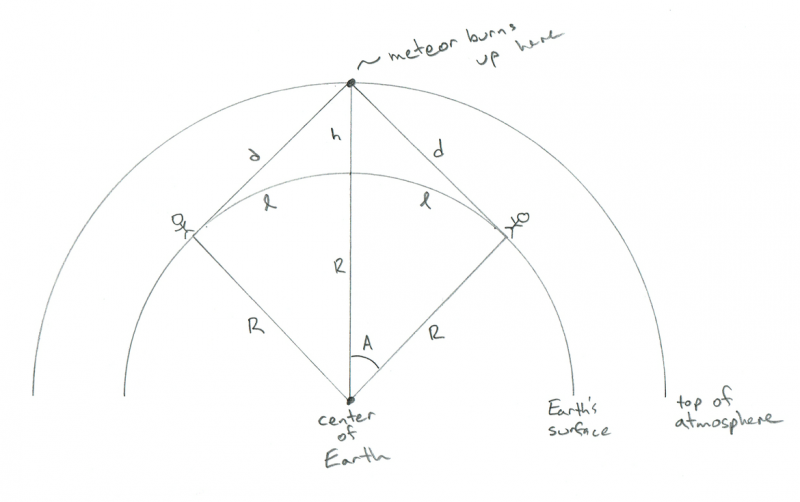
Schema, kurioje pavaizduota dviejų stebėtojų, stebinčių tiksliai tarp jų degantį meteorą, geometrija. Kreditas: Philas Plaitas
AHA! Dabar matai, kodėl aš noriu! Atstumas tarp dviejų žmonių yra tik 2 x l! Taigi dabar mes turime atsakymą:
Kad du žmonės matytų tą patį meteorą, vienas nuo kito gali būti ne daugiau kaip 2 x 1120 = 2240 kilometrų. Pavyzdžiui, tai yra gana arti atstumo tarp Vašingtono, DC ir Denverio. Oho.
Beje, norint pakeisti perspektyvą (pažodžiui), tai reiškia, kad meteoro požiūriu jis gali pamatyti 2240 kilometrų pločio Žemės ruožą (kaip DC rytinėje Žemės galūnėje ir Denveris vakarinėje). Tai gana šaunu.
angelo numeris 1111 meilė
Ir tai atneša mus į tikrąjį atsakymą į Deano klausimą: jei jis buvo 1000 km nuo savo šeimos, tada taip, techniškai jie galėjo pamatyti tą patį meteorą. Kaip apie tai?
Dabar tai daroma prielaida, kad oras yra visiškai skaidrus ir visa tai, kas iš tikrųjų yra neįmanoma. Taigi ši matematika atspindi idealią situaciją (įskaitant idėją, kad meteoras yra tiksliai tarp jų).
Būkime tikroviškesni. Tarkime, meteoras dega danguje 45 ° aukštyje virš horizonto abiem stebėtojams. Kaip toli jie būtų vienas nuo kito? Na, dar kartą darant prielaidą, kad meteoras yra tiksliai tarp jų, geometrija yra daugiau tokia:
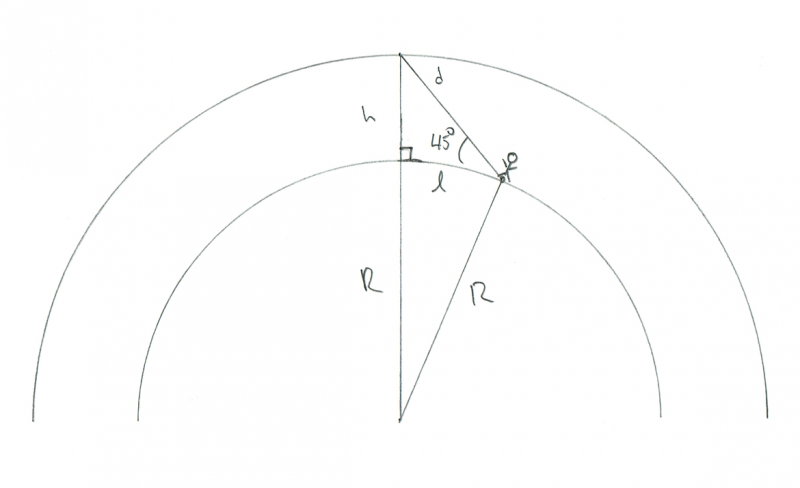
Schema, rodanti stebėtojo, stebinčio 45 ° virš horizonto degančio meteoro, geometriją. Kreditas: Philas Plaitas
Tai iš tikrųjų sunkiau išspręsti, bet žinau dar vieną triuką: jei manysime, kad l yra mažas, tada Žemės kreivumas nebus svarbus. Pavyzdžiui, jei noriu sužinoti atstumą tarp dviejų medžių savo kieme, man nerūpi, kad Žemė yra išlenkta. Per tokį mažą atstumą galiu daryti prielaidą, kad jis yra plokščias. Padarykime šią prielaidą čia.
Tokiu atveju turime kitą stačiakampį trikampį, tačiau šį kartą stačiasis kampas yra tas, kuris yra po meteoru. Aš netgi pažymėjau jį diagramoje mažu kvadratiniu užrašu. Taigi, jei tai 90 ° kampas, o mūsų kampas į meteorą yra 45 °, tada paskutinis kampas (nuo meteoro iki stebėtojo) taip pat yra 45 °. Tai reiškia, kad tai turi būti lygiašonis trikampis, taigi l ir h yra vienodi! Kadangi žinome, kad h yra 100 km, tai turi būti ir l.
O tai reiškia, kad atstumas tarp mūsų dviejų stebėtojų yra dvigubai didesnis, arba 200 km.
Beje, šiuo atveju atstumas iki meteoro yra apie 141 km. Patvirtinimą palieku skaitytojui kaip pratimą.
Iš esmės tai reiškia, kad jei žinote, kaip aukštai nuo horizonto yra meteoras ir koks aukštis jis sudegė, galite apskaičiuoti jo atstumą (arba jei žinote atstumą, galite gauti jo aukštį). Vis dėlto tas trigeris yra gana sudėtingas, ir manau, kad šiandien jums įmečiau pakankamai matematikos.
Bet šaunu galvoti, kad šiek tiek vidurinės mokyklos matematikos gali būti tokia smagi programa. Ir prisipažinsiu, poetiška ir romantiška žinoti, kad tol, kol išsiskyrimas nėra per toli, galima pasidalyti matančia krentančią žvaigždę su kuo nors kitu. Kokia miela mintis.
* In Ozo burtininkas , kaliausė suklydo po jis gavo smegenis.
† Apie žinoma Aš turiu mėgstamiausią trig tapatybę. Kas tavo?













